Una matrice è, analogamente ai vettori, una collezione finita di elementi omogenei, ossia dello stesso tipo, disposti secondo due dimensioni.
In generale, si utilizza il termine matrice per indicare gli array bidimensionali, ossia a due dimensioni, mentre le strutture con un numero di dimensioni superiore a due sono dette generalmente array n-dimensionali, sostituendo il valore di n con il numero delle dimensioni specifiche.

Ad ogni dimensione è associato un indice (zero-based come per i vettori) e, di conseguenza, per accedere ad ogni elemento della matrice occorre esplicitare i valori dei due indici, il primo per indicare la riga in cui si trova la cella a cui si vuole accedere ed il secondo per indicarne la colonna.

Graficamente possiamo sintetizzare quanto detto attraverso la figura seguente:

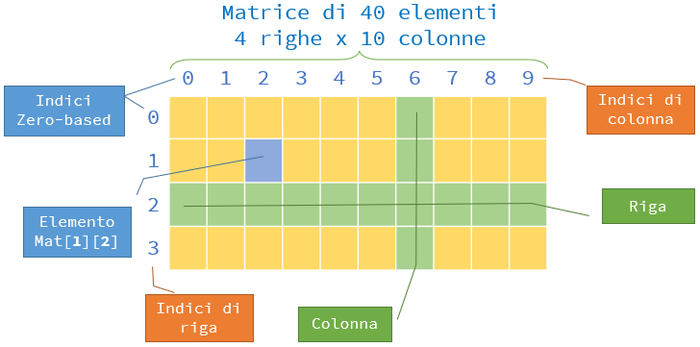
Se indichiamo con r il numero di righe di una matrice e con c il numero di colonne, si possono verificare i casi descritti di seguito:

• se r = 1 allora la matrice è costituita da un'unica riga e si definisce vettore riga
• se c = 1 allora la matrice è costituita da un'unica colonna e si definisce vettore colonna
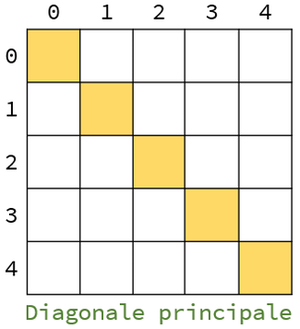
• se r = c allora la matrice è costituita dallo stesso numero di righe e colonne e si definisce matrice quadrata di ordine r o di ordine c
• se r <> c allora la matrice è costituita da un numero differente di righe e colonne e si definisce matrice rettangolare

La dichiarazione di una matrice deve specificare:

• il tipo degli elementi, seguito da una doppia coppia di parentesi quadre, aperta e chiusa, una per ogni dimensione, come mostrato nel seguito
• il nome della variabile o identificatore

Un esempio di dicharazione di una matrice è riportato nel seguente codice Java.

// dichiarazione di una matrice di interi
int[][] miaMatrice;

// Java permette di utilizzare anche 
// questa seconda sintassi

int miaMatrice[][];

In generale, la dichiarazione di una matrice deve avere la forma seguente:

// allocazione di una matrice di 10x5 interi
// ossia 10 righe e 5 colonne                            
miaMatrice = new int[10][5];

// allocazione di una matrice di 5x10 decimali
miaMatrice = new float[5][10];

Come mostrato per i vettori, anche per le matrici è possibile effettuare le operazioni di dichiarazione ed allocazione simultaneamente, come mostrato nel codice seguente.

// esempi di dichiarazione ed allocazione simultanea
int[][] miaMatrice = new int[10][5];

float[][] miaMatrice = new float[5][10];

Dopo aver dichiarato ed allocato una matrice è possibile accedere ai suoi elementi indicando, tra le parentesi quadre, che seguono il suo identificatore, i due indici, di riga e di colonna, che individuano la posizione dell'elemento.
Tali indici possono assumere, rispettivamente, i valori dell'intervallo 0 .. numero di righe - 1 e 0 .. numero di colonne - 1.

Quindi, per accedere al primo elemento della prima riga di una matrice di 5 righe per 10 colonne, occorrerà utilizzare l'istruzione

// dichiarazione ed allocazione di una matrice 
// di 10 righe e 5 colonne di numeri interi
int[][] miaMatrice = new int[10][5];

// scrittura del valore 50 nel primo elemento della seconda riga
miaMatrice[1][0] = 50; 

// scrittura del valore 100 nel terzo elemento della 5 riga
miaMatrice[4][2] = 100; 

// copia del valore del quinto elemento della seconda riga
// nel 10 elemento della 3 riga
miaMatrice[2][9] = miaMatrice[1][4];

// incremento del valore contenuto nel 5 elemento
// della 3 riga
miaMatrice[2][4]++;

// inizializzazione con valore 0 di tutti 
// gli elementi di una matrice di m righe ed 
// n colonne
for (int r = 0; r < m; r++) {
    for (int c = 0; c < n; c++) {
        miaMatrice[r][c] = 0;
    }
}

// stampa di tutti i valori contenuti
// in una matrice di m righe ed n colonne
for (int r = 0; r < m; r++) {
    for (int c = 0; c < n; c++) {
        // ipotizzando numeri di 3 cifre massimo ed interi
        System.out.printf("%4d", miaMatrice[r][c]);
    }
    System.out.println();
}

Anche nel caso della matrice, si può utilizzare la funzione length, per conoscere numero di righe o di colonne.

Vediamone un esempio, nel seguente frammento di codice Java.

// funzione che inizializza gli elementi 
// di una matrice con valore nullo
public static void azzeraMatrice(int[][] mat) {
    for (int r = 0; r < mat.length; r++) {
        for (int c = 0; c < mat[r].length; c++) {
            mat[r][c] = 0;
        }
    }
}

// funzione che stampa gli elementi di una matrice
// di cui non si conoscono a priori le dimensioni
public static void stampaMatrice(int[][] mat) {
    for (int r = 0; r < mat.length; r++) {
        for (int c = 0; c < mat[r].length; c++) {
            System.out.print(mat[r][c]+" ");
        }
        System.out.println();
    }
}

Abbiamo definito matrici quadrate, quelle matrici che hanno lo stesso numero di righe e di colonne.
Nell'ambito delle matrici quadrate possiamo individuare gli elementi che compongono la diagonale principale e la diagonale secondaria della matrice.

Tali elementi sono evidenziati nelle figure che seguono:

Se consideriamo, invece, i valori contenuti nelle celle della matrice, possiamo allora avere le classificazioni che seguono:

• matrice nulla, ossia con tutti gli elementi nulli
  
• matrice diagonale, ossia con tutti gli elementi nulli tranne quelli della diagonale principale
  
• matrice scalare di ordine n, ossia con tutti gli elementi nulli tranne quelli della diagonale principale, contenenti il valore numerico n
  
• matrice unitaria, ossia con tutti gli elementi nulli tranne quelli della diagonale principale, contenenti il valore numerico uno. Questo tipo di matrice si può anche definire, sulla base di quanto detto finora, scalare di ordine 1
  
• matrice simmetrica, ossia speculare rispetto alla diagonale principale, o in altri termini tale che soddisfi la seguente condizione mat[r][c] = mat[c][r]
  
  
• matrice triangolare superiore, ossia con tutti gli elementi al di sotto della diagonale principale nulli e quelli al di sopra non tutti nulli. In formule:
  mat[r][c] != 0 se r <= c
  mat[r][c] = 0 se r > c
  
  
• matrice triangolare inferiore, ossia con tutti gli elementi al di sopra della diagonale principale nulli e quelli al di sotto non tutti nulli. In formule:
  mat[r][c] != 0 se r >= c
  mat[r][c] = 0 se r < c